Physics 1st Year Chapter 2 MCQs are up-to-date and are beneficial for both entry tests and board examinations. Students must prepare these again and again to have the best possible result.
Physics 1st Year Chapter 2 MCQs
FSc 1st Year Physics Chapter 2 MCQs Notes are a helping material for all kinds of papers.
Physics 1st Year Chapter 2 Vectors and Equilibrium
Which one is a vector:
An example of scalar quantity is:
Name the quantity which is vector:
Rectangular coordinate system is also called:
The direction of a vector in space is specified by:
If both components of a vector are negative, then resultant lies in:
In which quadrant the two rectangular components of a vector have same sign?
If the x-component of a vector is positive and y- component is negative, then resultant vector lies in what quadrant:
If vector A lies in the third quadrant, its direction will be:
A single vector having the same effect as all the original vectors taken together, is called:
When two vectors are anti-parallel, the angle between them is:
The resultant of two forces 30 N and 40 N acting at an angle of 90° with each other is:
The magnitude of the vector 2/3 ı̂ − 1/3 Ĵ + 2/3 k^ is:
If 6N force act at right angle to 8N force, then the magnitude of resultant will be:
If A¯ + B¯ = ¯B + ¯A, this shows that addition of vectors is:
A body is in dynamic equilibrium only when it is:
The unit vector along y-axis is:
Mathematically, unit vector is described as:
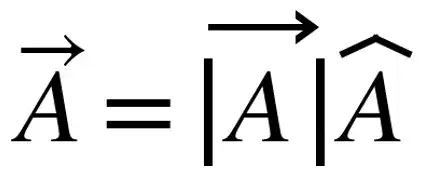
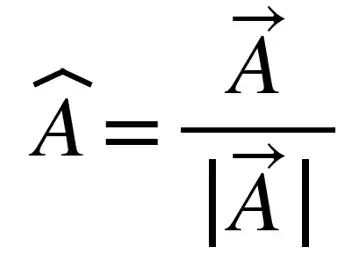
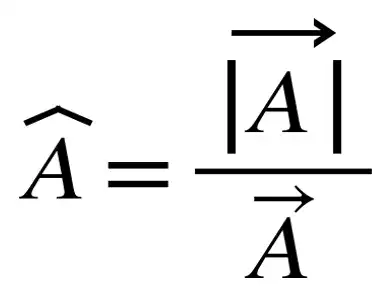
A unit vector is obtained by dividing a vector with:
The unit vector in the direction of vector A = 2ı̂ − 2Ĵ + k^ is:
The magnitude of a vector ¯A = Ası̂ − AyĴ:
Vectors A is along y axis, its component along x axis is:
The angle between rectangular components of vector:
A force of 10N is acting along x-axis, its component along y-axis is:
If vector A is acting along y-axis, its y-component is:
If A = 2ı̂ − Ĵ + 3k^, then the magnitude of vector A is:
| ı̂ − Ĵ − 3k^| =
If A = 2ı̂ + Ĵ + 2k^, then |A| is :
Dot product of two non-zero vectors is zero, when angle between them is:
The cross product ı̂ × ı̂ = Ĵ × Ĵ = k^ × k^ is equal to:
The scalar product of two vectors is maximum when they are:
Two vectors A and B are making angle θ with each other. The projection of vector B on vector A is written as.:
The projection of a vector ¯B over ¯A is:
If A = Ası̂ + AyĴ + Azk^ and B = Bsı̂ + ByĴ + Bzk^ then:
The magnitude of vector product is given by:
The direction of vector product is given by:
The cross product ı̂ × Ĵ is equal to:
Torque has zero value, if the angle between r̅ and F¯ is:
ı̂. (Ĵ × k^) is equal to:
The cross product of vectors will be minimum when the angle between vectors is:
The direction of torque is:
¯A × ¯A is:
If the position r̅ and force F¯ are in same direction, then torque will be:
The direction of torque can be found by:
At what angle, the two vectors of the same magnitude have to oriented, if they were to be combined to give a resultant equal to a vector of same magnitude?
If the line of action of force passes through axis of rotation or the origin, then its torque is:
The magnitude of a vector can never be:
The minimum number of unequal forces whose resultant will be zero:
Torque is defined as:
SI unit of torque is:
A body will be in complete equilibrium when it is satisfying:
If a body is at rest, then it will be in:
The magnitudes of rectangular component are equal if its angle with x-axis is:
If Ax = Ay, then the angle between the vector A with x-axis will be:
The resultant of two forces of equal magnitudes is also equal to the magnitude of the forces. The angle between the two forces is:
The magnitude of dot and cross product of two vectors are 6√3 and 6 respectively. The angle between them will be:
The magnitude of cross-product and dot-product of two vectors are equal, the angle between them is:
Two vectors to be combined have magnitudes 60 N and 35 N. The correct answer for the magnitude of their resultant will be:
Physics 1st Year Chapter 2 Vectors and Equilibrium
You got {{userScore}} out of {{maxScore}} correct
{{title}}
{{image}}
{{content}}
Solve More Chapters’ MCQs Online




